Gradient Descent: Newton and Quasi-Newton Method
Newton’s Method
Different from gradient-descent (GD) method which tries to directly converge the design variable to a minimiser, Newton’s method uses an important characteristic of an extreme value – gradient of the function ($\nabla \mathbf{f}$) equals zero. While GD has a first-order convergence, Newton’s method has second-order convergence, which means it suffers less severe zig-zag problems.
Recall our primary school math, that we can find the root of an equation $f=0$ by $$ x_{k+1} = x_k - \frac{f}{f^\prime}. $$
Similarly, we can find the root of $f^\prime=0$ by $$ x_{k+1} = x_k - \frac{f^\prime}{f^{\prime\prime}}. \label{eqn:-1} $$
Rearrange \eqref{eqn:-1} and extend to higher dimension, and we can obtain $$ \mathbf{H}\Delta\mathbf{x_k}=-\nabla\mathbf{f}\left(\mathbf{x} _{k}\right). \label{eqn:-2} $$ \eqref{eqn:-2} is the update formula for Newton’s method.
Quasi-Newton Method
In Newton’s method, the inverse of Hessian ($\mathbf{H}^{-1}$) is required. For a large-scale optimisation problem, the number of variables ($n$) can be very large, and the size of the Hessian ($n\times n$) is even larger. Inverting the Hessian matrix can be thus very expensive. In Quasi-Newton method, the Hessian is approximated instead of directly computed, by an iterative process, which is much computationally cheaper.
Lemma: Broyden Root-Finding Method
For scalar functions ($\mathbb{R}\to\mathbb{R}$), it is possible to approximate the gradient of a function by solving $$ \mathbf{J} _{k}\left(\mathbf{x} _{k}-\mathbf{x} _{k-1}\right)=\mathbf{F}\left(\mathbf{x} _{k}\right)-\mathbf{F}\left(\mathbf{x} _{k-1}\right). \label{eqn:1} $$ where $J _{k}$ is the approximated gradient.
However, this does not work in vector-valued functions ($\mathbb{R}^n\to\mathbb{R}^n$), because we are solving $\mathbf{J}_{k}$, an $n\times n$ matrix, by only $n$ equations. Graphically, we cannot find the gradient in all directions by only draw one secant line of the function.
However, we still want to find a way to approximate $\mathbf{J}_{k}$ iteratively, if the straightforward approach is impossible. The goal is to solve $$ \mathbf{J} _{k} \mathbf{s} _{k}=\Delta \mathbf{F} _{k}, \label{eqn:2} $$ where $\mathbf{s} _{k}=\mathbf{x} _{k}-\mathbf{x} _{k-1}$ and $\Delta \mathbf{F} _{k}=\mathbf{F}\left(x _{k}\right)-\mathbf{F}\left(x _{k-1}\right)$.
One way to update $\mathbf{J} _{k}$ is $$ \mathbf{J} _{k}=\mathbf{J} _{k-1}+\frac{\Delta \mathbf{F} _{k}-\mathbf{J} _{k-1} \mathbf{s} _{k}}{\left|\mathbf{s} _{k}\right|^{2}} \mathbf{s} _{k}^{\top}. \label{eqn:3} $$
It can be seen that \eqref{eqn:2} and \eqref{eqn:3} are consistent. In addition, \eqref{eqn:3} tries to minimise the Frobenius norm (elementwise L2 norm) of $\left|\mathbf{J} _{k}-\mathbf{J} _{k-1}\right| _F$. Once we have $\mathbf{J} _{k}$, we can update $\mathbf{x} _{k}$ by \eqref{eqn:1}.
However, note that only $\mathbf{J}^{-1} _{k}$ is required in \eqref{eqn:1} and inverting the Jacobian at each iteration is expensive for a large $n$. It is desired to update $\mathbf{J}^{-1} _{k}$ directly.
Here, we apply the Sherman-Morrison formula, which reads $$ \left(A+u v^{\top}\right)^{-1}=A^{-1}-\frac{A^{-1} u v^{\top} A^{-1}}{1+v^{\top} A^{-1} u}. $$
We can now express \eqref{eqn:1} by $$ \mathbf{J} _{k}^{-1}=\mathbf{J} _{k-1}^{-1}+\frac{\Delta \mathbf{x} _{k}-\mathbf{J} _{k-1}^{-1} \Delta F _{k}}{\Delta \mathbf{x} _{k}^{\top} \mathbf{J} _{k-1}^{-1} \Delta F _{k}} \Delta \mathbf{x} _{k}^{\top} \mathbf{J} _{k-1}^{-1}. \label{eqn:4} $$
We will store $\mathbf{J} _{k-1}^{-1}$ in the memory and update $\mathbf{J} _{k}^{-1}$ by evaluating \eqref{eqn:4} repeatedly.
Broyden–Fletcher–Goldfarb–Shanno (BFGS) Algorithm
Similar to the Broyden root-finding method, BFGS method approximates Hessian in \eqref{eqn:-2} by $$ \mathbf{B} _{k} \mathbf{s} _{k}=-\nabla \mathbf{f}\left(\mathbf{x} _{k}\right) $$ where $\mathbf{B} _{k}$ is the approximated Hessian, $\mathbf{s} _{k}$ is the step, and RHS is the gradient of the objective function.
First, we need an initial guess for $\mathbf{B} _{k}$ so that we can calculate $\mathbf{s} _{k}$ – this linear system is deterministic. Then, we can update $\mathbf{x}$ by $$ \mathbf{x} _{k+1}=\mathbf{x} _{k}+\mathbf{S} _{k}. $$
We also denote the change of gradient $$ \mathbf{y} _{k}=\nabla \mathbf{f}\left(\mathbf{x} _{k+1}\right)-\nabla \mathbf{f}\left(\mathbf{x} _{k}\right). $$
Similar to \eqref{eqn:2}, we need to choose an update formula for $\mathbf{B} _{k}$ to be $$ \mathbf{B} _{k+1} \mathbf{s} _{k}=\mathbf{y} _{k}. \label{eqn:5} $$
To ensure $\mathbf{B}_k$ is symmetric positive definite (SPD), we can enforce the following update rule $$ \mathbf{B} _{k+1}=\mathbf{B} _{k}+\alpha \mathbf{u}^{} \mathbf{u}^{\top}+\beta \mathbf{v}^{} \mathbf{v}^{\top}. \label{eqn:6} $$
For \eqref{eqn:6} to satisfy \eqref{eqn:5}, we try $\mathbf{u}=\mathbf{y} _{k}$ and $\mathbf{v}=\mathbf{B} _{k} \mathbf{s} _{k}$ and see whether we can find a possible $\alpha$ and $\beta$ value. Now, \eqref{eqn:6} becomes $$ \mathbf{B} _{k+1}=\mathbf{B} _{k}+\alpha \mathbf{y} _{k} \mathbf{y} _{k}^{\top}+\beta \mathbf{B} _{k} \mathbf{s} _{k} \mathbf{s} _{k}^{\top} \mathbf{B} _{k}. $$
To be consistent with \eqref{eqn:5}, we need $$ \color{CadetBlue}{\mathbf{y} _{k}}=\mathbf{B} _{k+1} \mathbf{s} _{k}=\color{DarkSalmon}{\mathbf{B} _{k} \mathbf{s} _{k}}+\color{CadetBlue}{\alpha \mathbf{y} _{k} \mathbf{y} _{k}^{\top} \mathbf{s} _{k}}+\color{DarkSalmon}{\beta \mathbf{B} _{k} \mathbf{s} _{k} \mathbf{s} _{k}^{\top} \mathbf{B} _{k} \mathbf{s} _{k}}. $$
Matching terms in the same colour and we obtain $$ \alpha=\frac{1}{\mathbf{y} _{k}^{\top} \mathbf{s} _{k}}, \quad \beta=-\frac{1}{\mathbf{s} _{k}^{\top} \mathbf{B} _{k} \mathbf{s} _{k}}. $$
Hence, the update formula for approximated Hessian is $$ \mathbf{B} _{k+1}=\mathbf{B} _{k}+\frac{\mathbf{y} _{k} \mathbf{y} _{k}^{\top}}{\mathbf{y} _{k}^{\top} \mathbf{s} _{k}}-\frac{\mathbf{B} _{k} .\mathbf{s} _{k} \mathbf{s} _{k}^{\top} \mathbf{B} _{k}}{\mathbf{s} _{k}^{\top} \mathbf{B} _{k} \mathbf{s} _{k}}. $$
Similarly, we also want to update the $\mathbf{B}^{-1} _{k}$ if possible. Using Sherman-Morrison formula again, without a step-by-step derivation, we reach $$ \Delta \mathbf{H} _{k}=\left(\mathbf{I}-\mathbf{s} _{k} \rho _{k} \mathbf{y} _{k}^{\top}\right) \mathbf{H} _{k}\left(\mathbf{I}-\rho _{k} \mathbf{y} _{k} \mathbf{s} _{k}^{\top}\right)+\rho _{k} \mathbf{s} _{k} \mathbf{s} _{k}^{\top} $$ where $\rho _{k}=\dfrac{1}{\mathbf{y} _{k}^{\top} \mathbf{s} _{k}}$ is a scalar.
A Sample Study
The above mentioned methods are implemented in a Julia package Optim.jl. Here we use this package to optimise the Rosenbrock function
$$
f(x,y) = (1 - x)^2 + 100.0 (y - x^2)^2.
$$
We use Gradient Descent method (introduced in the previous blog), both with and without line search, and BFGS optimiser. The results is shown in the following figure:
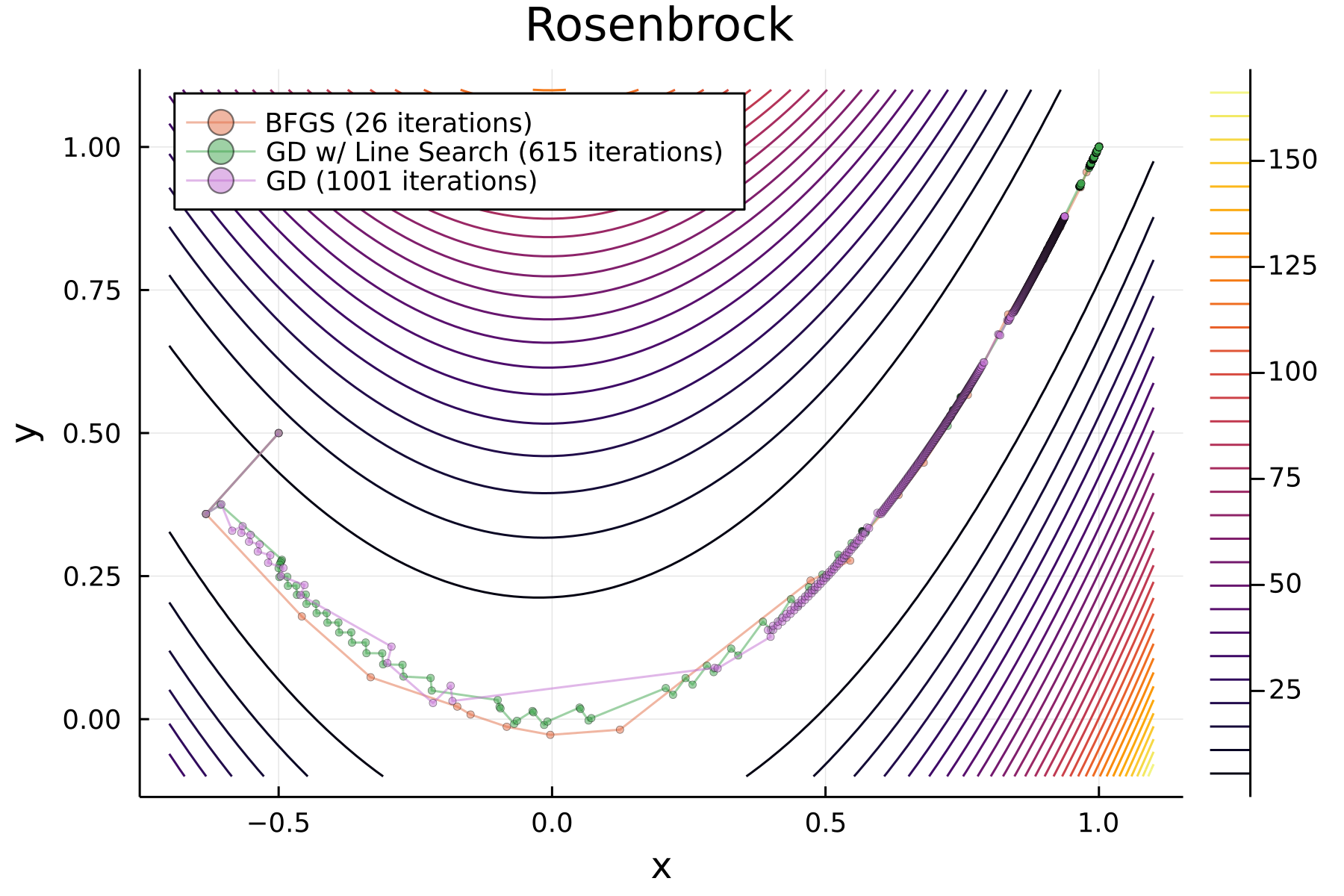
It can be clearly seen that BFGS performs the best, converging to the global minimum $(1,1)$ with 26 iterations. GD with line search requires 615 iterations, a significant larger number, also converging to the correct value. However, the vanilla GD method uses 1000 iterations and still cannot converge to the minimum.
using Optim
using Plots
using LineSearches
f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
x = LinRange(-0.7, 1.1, 101)
y = LinRange(-0.1, 1.1, 101)
fig = plot(dpi=300, title="Rosenbrock", xlabel="x", ylabel="y", legend=:topleft)
fig = contour!(x, y, (x,y) -> f([x,y]), levels=30)
start = [-0.5, 0.5]
res1 = optimize(f, start, BFGS(),
Optim.Options(
store_trace=true,
extended_trace=true,
)
)
trace1 = mapreduce(permutedims, vcat, Optim.x_trace(res1))
fig = plot!(trace1[:,1], trace1[:,2], marker=:circle, label="BFGS ($(size(trace1,1)) iterations)", alpha=0.5, markersize=2, markeralpha=0.5, markerstrokewidth=0.3)
algo_gd_hz = GradientDescent(;alphaguess = LineSearches.InitialStatic(), linesearch = LineSearches.HagerZhang())
res2 = optimize(f, start, algo_gd_hz,
Optim.Options(
store_trace=true,
extended_trace=true,
)
)
trace2 = mapreduce(permutedims, vcat, Optim.x_trace(res2))
fig = plot!(trace2[:,1], trace2[:,2], marker=:circle, label="GD w/ Line Search ($(size(trace2,1)) iterations)", alpha=0.5, markersize=2, markeralpha=0.5, markerstrokewidth=0.3)
res3 = optimize(f, start, GradientDescent(),
Optim.Options(
store_trace=true,
extended_trace=true,
)
)
trace3 = mapreduce(permutedims, vcat, Optim.x_trace(res3))
fig = plot!(trace3[:,1], trace3[:,2], marker=:circle, label="GD ($(size(trace3,1)) iterations)", alpha=0.5, markersize=2, markeralpha=0.5, markerstrokewidth=0.3)